Balmoral Software
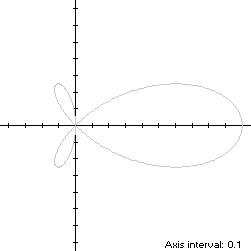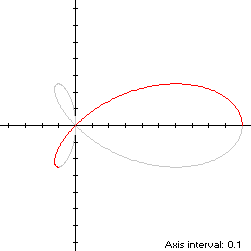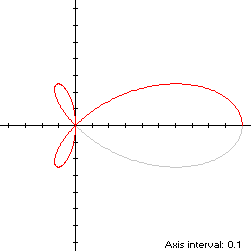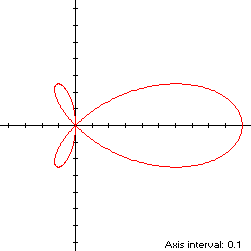
Balmoral Software

r(t) = cos(t)cos(2t)for t ∈ T = [0,π). The curve always moves counterclockwise, visiting the origin three times, hence its name. At
 at
at  at
at
 at
at r'(t) = -[sin(t) + 3sin(3t)]/2,so by (L2), the perimeter of S is
Its centroid abscissa is 1/2.
 and one vertical line segment
of length
and one vertical line segment
of length  By
(L2), the perimeter of the convex hull
consists of these line segments plus the arc of a thin wedge in each small lobe
and the convex portion of the main lobe:
By
(L2), the perimeter of the convex hull
consists of these line segments plus the arc of a thin wedge in each small lobe
and the convex portion of the main lobe:
The perimeter of the convex hull is about 16% shorter than that of the trefoil.
In the upper half-plane, the line segments of the convex hull create two triangles, shown in blue in the left diagram at the bottom of this page. At left is a right triangle of area
and whose centroid abscissa -1/12 is the average of its vertex abscissas. At the top is a scalene triangle with area
and centroid abscissa 1/6. By (A2), the thin wedge of the small lobe has area
By (C1), its centroid abscissa is
Similarly, the area of the convex portion of the main lobe in the upper half-plane is
and its associated centroid abscissa is
The component metrics for half of the convex hull can be summarized as follows:
The total area of the convex hull is 0.521114, about 1/3 larger than that of the trefoil. The centroid abscissa of the convex hull is the weighted average
Region Area Centroid abscissa Product Right triangle -1/12 Small lobe wedge Scalene triangle 1/6 Main lobe portion Total
x(t) = r(t)cos(t) = cos2(t)cos(2t)Using z = 1 in Lemma C,y(t) = r(t)sin(t) = sin(4t)/4
[x2(t) + y2(t) - z2]/[x(t) - z]/2 = cos(2t)/2 + 1/[cos(2t) + 2]is minimized at
For verification, we have
a = 0.698874It's interesting to note that the circumellipse's center abscissa c is the same as its half-height b in this optimal solution.b = 0.312453
c = 0.312454
d = 0
d/dt [x(t) - z]y(t) = d/dt [cos2(t)cos(2t) - 1]sin(4t)/4has a zero at t* = 0.538406 radians. The corresponding coordinates are
x* = 0.349472We then havey* = 0.208727
For verification,
 when
when
Since the trefoil is defined by a polar function, tR is also the clockwise rotation angle. The parametric coordinate functions of the rotated curve are:
The asymmetry can then be seen by comparing the upper half of the lobe (red) with a reflection of the lower half (blue):
R = 0.038767c = -0.070559
d = -0.160962
a = 0.111756To display the tilted ellipse in the upper tail lobe, the axis-aligned ellipse is rotated counterclockwise byb = 0.036490
c = 0.160167
d = -0.001576
Figure Parameters Perimeter Area Centroid Incircle (tail) R = 0.038767 0.243580 0.004721 (-0.070559,-0.160962) Inellipse (tail) * a = 0.111756
b = 0.0364900.496259 0.012811 (0.160167,-0.001576) Incircle (main lobe) R = 1/4 1.570796 0.196350 (0.603553,0) Inellipse (main lobe) a = 0.433685
b = 0.2410172.163075 0.328376 (0.566315,0) Trefoil Width: 9/8
Height: 1/23.54166 0.392699 (0.5,0) Convex hull 2.968856 0.521114 (0.400239,0) Circumellipse a = 0.698874
b = 0.3124533.294240 0.686015 (0.312454,0) Circumcircle 3.680605 1.078024 (0.414214,0) *: With respect to rotated curve S
The trefoil (red) is similarly shaped to the fish curve:
Copyright © 2021 Balmoral Software (http://www.balmoralsoftware.com). All rights reserved.