Teardrop Curve

Teardrop Curve TEARDROP CURVE

Balmoral Software

A second-order teardrop curve opening to the right is a non-convex x-symmetric closed curve with parametric equations

x(t) = -cos(t)
y(t) = sin(t)sin²(t/2), 0 ≤ t < 2π

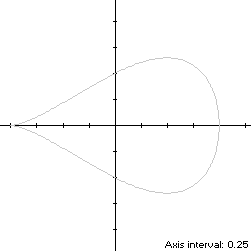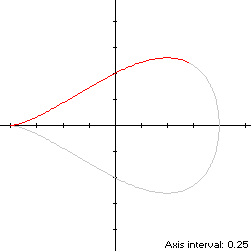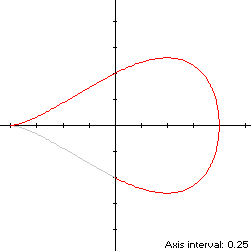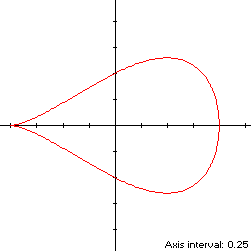
The curve follows a clockwise path as t increases, starting from the left cusp at (x(0),y(0)) = (-1,0). Its extreme abscissas occur at the cusp and at (1,0) when t = π. The maximum ordinate of the teardrop curve occurs at

when t = 2π/3, so the width x height of its bounding rectangle is

Metrics

We have

x'(t) = sin(t)
y'(t) = [cos(t) - cos(2t)]/2

so by (L1), the perimeter of the teardrop curve is

and its area is

By (C1), its centroid abscissa is

(Note: WolframAlpha has reversed the coefficients.)

Convex Hull

We have

x''(t) = sin(t)
y''(t) = sin(2t) - sin(t)/2,

so by (X1), the teardrop curvature changes sign at (-1,0) since

sin(t)[sin(2t) - sin(t)/2] = cos(t)[cos(t) - cos(2t)]/2

is satisfied for t = 0. Equation (X2) is evaluated with respect to the point (-1,0) as

which has a solution in the upper half-plane at t = π/2, so the convex hull line segments extend between the points (-1,0) and (x(π/2),±y(π/2)) = (0,±1/2). These line segments are shown in blue in the left diagram below, and each has length

By (L1), the perimeter of the convex hull is:

which is less than 1% shorter than that of the teardrop curve.

The line segments of the convex hull create an isosceles triangle with its base on the y-axis, having area 1/2. The centroid abscissa of this triangle is the average of its vertex abscissas, or -1/3. By (A1), the remainder of the convex hull has area

By (C1), the associated centroid abscissa is

The convex hull component metrics can be summarized as follows:

Region Area Centroid abscissa Product

Triangle 1/2 -1/3 -1/6

Remainder A = 1/3 + π/4 (1/3 + π/16)/A 1/3 + π/16

Total 5/6 + π/4 1/6 + π/16

Region	Area	Centroid abscissa	Product
Triangle	1/2	-1/3	-1/6
Remainder	A = 1/3 + π/4	(1/3 + π/16)/A	1/3 + π/16
Total	5/6 + π/4		1/6 + π/16

The area of the convex hull is 1.618732, about 3% larger than that of the teardrop curve. The centroid abscissa of the convex hull is the weighted average

which is 1/(20 + 6π) to the left of the centroid of the teardrop curve itself, exactly the same distance as the corresponding value for the piriform curve.

Incircle

The maximum ordinate

of the teardrop curve does not define its inradius since the corresponding abscissa 1/2 is too close to the right edge (1,0), so its incircle is constrained by the right edge. Using z = 1 in Lemma C, we have

and R = |c - z| =

. For verification, we have

Inellipse

Using z = 1 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt -sin³(t)/2

has a zero at t* = π/2. The corresponding coordinates are

x* = 0
y* = 1/2,

which is the endpoint of a convex hull line segment. We then have

For verification,

Circumellipse

Using z = -1 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt 2sin⁴(t/2)sin(t)

has a zero at t* = Arccos(-2/3). The corresponding coordinates are

from which we have

For verification,

Circumcircle

Since the abscissa extrema are on the x-axis and the bounding rectangle is wider than it is tall, a candidate for the circumcircle has radius R = 1 and center at the origin. For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 3.864786 1.188615 (0.384900,0)

Inellipse 3.913233 1.209200 (0.333333,0)

Teardrop curve 5.13734 1.570796 (0.25,0)

Convex hull 5.127128 1.618732 (0.224260,0)

Circumellipse 5.810712 2.503567 (1.111111,0)

Circumcircle R = 1 6.283185 3.141593

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R =	3.864786	1.188615	(0.384900,0)
Inellipse		3.913233	1.209200	(0.333333,0)
Teardrop curve		5.13734	1.570796	(0.25,0)
Convex hull		5.127128	1.618732	(0.224260,0)
Circumellipse		5.810712	2.503567	(1.111111,0)
Circumcircle	R = 1	6.283185	3.141593

The teardrop curve (red) is a member of a group of similarly-shaped figures described on these pages, including (inside to outside) the Tschirnhausen cubic, the right strophoid, the Trisectrix of Maclaurin and the piriform curve:

Relationship with the piriform curve

The teardrop curve coincides with the piriform curve after translating its abscissas to the right by 1 and doubling its ordinates. The transformed coordinate functions are

x₁(t) = x(t) + 1 = 1 - cos(t)
y₁(t) = 2y(t) = 2sin(t)sin²(t/2)

These coordinate functions cannot be directly compared with the corresponding ones for the piriform curve since the rates of travel along the path T (if t is considered a time variable) vary between the two curves. However, the path itself is the same for both curves since x₁(t), y₁(t) satisfy the cartesian form of the piriform curve:

y² = x³(2 - x)

Top Page

Home