Right Strophoid

Right Strophoid RIGHT STROPHOID

Balmoral Software

The lobe of the right strophoid is a convex x-symmetric droplet-shaped closed curve S with polar equation

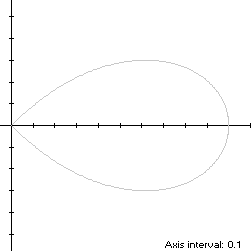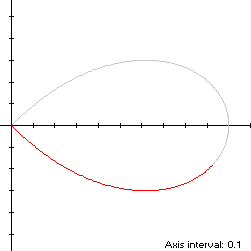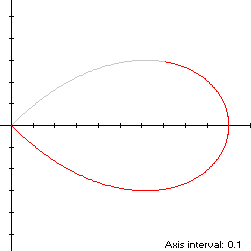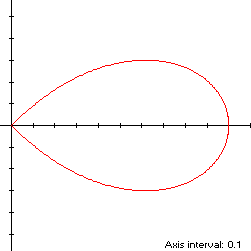
r(t) = 2cos(t) - sec(t), -π/4 ≤ t < π/4

The curve follows a counterclockwise path as t increases, starting from the cusp at the origin when t = -π/4, proceeding through Quadrant IV to the right edge (1,0) at t = 0, then following a symmetric path through Quadrant I back to the cusp at t = π/4. The maximum ordinate point of S is

so the width x height of its bounding rectangle is

Metrics

The area of S is

A = (4 - π)/2

We have

r'(t) = -2sin(t) - tan(t)sec(t),

so by (L2), the perimeter of S is

By (C2), its centroid abscissa is

Incircle

The maximum radius of a circle centered on the x-axis and inscribed in S is its maximum ordinate, so a candidate for the incircle has radius

and center abscissa

The candidate circle must be contained within S, so we require that c - R and c + R both be within the abscissa range [0,1] of S, which is true. For verification, we have

Inellipse

Using z = 1 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt -2sin²(t)cos(2t)tan(t)

has a zero at

The corresponding coordinates are

We then have

For verification,

Circumellipse

Using z = 0 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt cos²(2t)tan(t)

has a zero at

The corresponding coordinates are

We then have

For verification,

Circumcircle

Since the abscissa extrema are on the x-axis and the bounding rectangle is wider than it is tall, a candidate for the circumcircle has its radius and center abscissa both equal to 1/2. For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 1.886734 0.283277 (0.618034,0)

Inellipse 2.252459 0.382312 (0.577350,0)

Right strophoid 2.4896 0.429204 (0.553264,0)

Circumellipse 2.668302 0.517274 (0.520518,0)

Circumcircle R = 1/2 3.141593 0.785398 (0.5,0)

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R =	1.886734	0.283277	(0.618034,0)
Inellipse		2.252459	0.382312	(0.577350,0)
Right strophoid		2.4896	0.429204	(0.553264,0)
Circumellipse		2.668302	0.517274	(0.520518,0)
Circumcircle	R = 1/2	3.141593	0.785398	(0.5,0)

The right strophoid (red) is a member of a group of similarly-shaped figures described on these pages, including (inside to outside) the teardrop curve, the Tschirnhausen cubic, the Trisectrix of Maclaurin and the piriform curve:

Top Page

Home