Circular Sector

Circular Sector CIRCULAR SECTOR

Balmoral Software

Let a circular sector S of radius 1 be oriented with the origin at the midpoint of the chord connecting the endpoints of its arc, and with the center of the circle on the negative y-axis, so that S is symmetric with respect to that axis. If β < π/2 is one-half the angle subtended by the sector arc, then the extreme abscissa points of S are (±sin(β),0), the minimum ordinate point is (0,-cos(β)), the maximum ordinate point is (0,1 - cos(β)), and the width x height of the bounding rectangle of S is 2sin(β) x 1.

Let t represent the usual parameter, ranging from 0 to 2π through the quadrants in counterclockwise order. In Quadrants I and II, the parametric equations of the sector arc are:

x(φ) = cos(φ)
y(φ) = sin(φ) - cos(β),

where the angle φ is measured from the center of the circle and ranges from π/2 - β to π/2 + β. We can scale t to the angular parameter φ as follows:

Range of t Range of φ

[0,π] [π/2 - β,π/2 + β]

or equivalently,

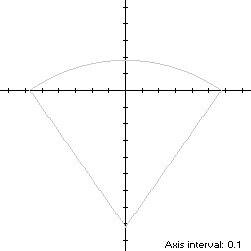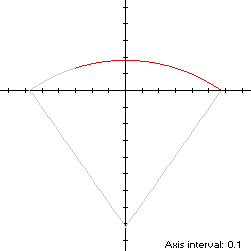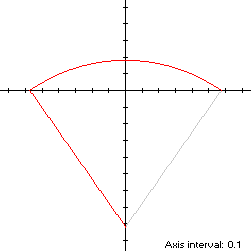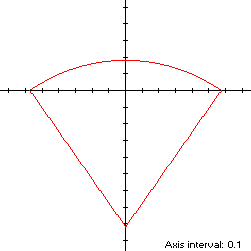
φ = 2βt/π + π/2 - β

In Quadrants III and IV, S consists of symmetric line segments joining the points (-sin(β),0), (0,-cos(β)) and (sin(β),0), so the parametric functions are linear in t. Combining definitions, we have

Metrics

The perimeter of the sector is the length of the circular arc (in radians) plus its two radii:

L = 2β + 2

The area A of S is β radians and its centroid ordinate is

Specific Example

In the remainder of this paper, we use

β = 35° = 7π/36
L = 3.221731
A = 0.610865
d = -0.193180
Bounding rectangle: 1.147153 x 1

Incircle

Using z = 1 - cos(β) in Lemma C, we have

R = |d - z| = 0.364505

For verification, we have

Inellipse

Using z = 1 - cos(β) in Lemma E,

d/dt x(t)[y(t) - z] = d/dt (2t/π - 3)sin(β)[|2t/π - 3|cos(β) - 1]

has a zero in [π,2π) when

The corresponding coordinates are

We then have

For verification,

Circumcircle

A circumcircle passing through the three corners of S will have a smaller radius than that of the sector itself, and so will have a greater curvature and contain the circular arc portion of S. Applying Lemma TC to an inverted acute isosceles triangle with h = cos(β) and w = 2sin(β), the center ordinate (negated) and the radius of the circumcircle are:

d = h/2 - w²/(8h) = cos(2β)sec(β)/2 = -0.208765
R = h - d = sec(β)/2 = 0.610387

Circumellipse

Using the same approach as for the circumcircle, we apply Lemma TE with h = cos(β) and w = 2sin(β) to find the parameters of the circumellipse:

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 0.364505 2.290253 0.417404 (0,-0.183657)

Inellipse a = tan(7π/36)/\/3
b = 1/3 2.322593 0.423345 (0,-0.152485)

Circular sector Width: 2sin(β)
Height: 1 3.221731 0.610865 (0,-0.193180)

Circumellipse a =
b = 3.805114 1.136275 (0,-0.273051)

Circumcircle R = sec(β)/2 3.835177 1.170472 (0,-0.208765)

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 0.364505	2.290253	0.417404	(0,-0.183657)
Inellipse	a = tan(7π/36)/\/3 b = 1/3	2.322593	0.423345	(0,-0.152485)
Circular sector	Width: 2sin(β) Height: 1	3.221731	0.610865	(0,-0.193180)
Circumellipse	a = b =	3.805114	1.136275	(0,-0.273051)
Circumcircle	R = sec(β)/2	3.835177	1.170472	(0,-0.208765)

Top Page

Home