Rose

Rose ROSE

Balmoral Software

A three-lobed rose with a petal on the positive x-axis is a closed curve S with polar equation

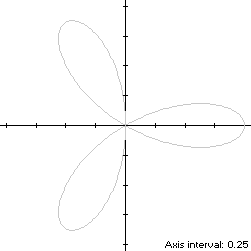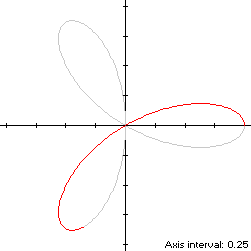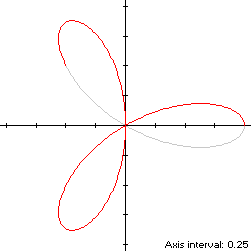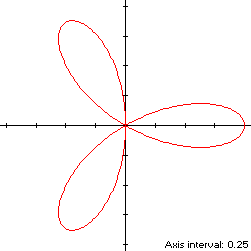
r(t) = cos(3t), 0 ≤ t < π

This curve is also known as the trifolium. Movement along S is always counterclockwise, starting at its maximum abscissa point (1,0) and crossing the origin three times. There are two minimum-abscissa points

the lower of which occurs at

so S is non-convex by the multiple local extrema test. The ordinate extrema of S are

so the width x height of its bounding rectangle is

Symmetry

Since

r(t + 2π/3) = cos(3t + 2π) = r(t),

the condition (R2) of Lemma R is satisfied and the rose is rotationally symmetric with period 2π/3.

Metrics

The perimeter of the rose is 6.682447 and its area is π/4.

Convex Hull

The convex hull is created by connecting the minimum abscissa points with a vertical line segment of length

and then repeating the pattern by rotating around the origin at 2π/3 intervals. The far end of the lower-left rose petal is reached at t = π/3, so the rounded edge of the petal that occurs for values of t between t₁ and π/3 is part of the convex hull, and there are 6 such parts by symmetry. We have

r'(t) = -3sin(3t),

so by (L2), the perimeter of the convex hull is

which is about 20% shorter than that of the rose.

The line segments of the convex hull create three isosceles triangles with the origin, each having an area of

as shown in blue in the left diagram below. By (A2), the area of the convex hull is

which is a little over twice the area of the rose.

Circumconics

Since the rose is rotationally symmetric with period 2π/3, its circumcircle and circumellipse are the same. The squared-distance function of S

r²(t) = cos²(3t)

is maximized at 1, so that is the circumradius.

Incircle (lobe)

Consider the x-symmetric right lobe of the rose, where -π/6 ≤ t < π/6. The maximum ordinate point on this lobe is (c,R), where

and

The largest circle centered on the x-axis and inscribed in the lobe has radius R and center abscissa c. The circle must be contained within the lobe, so we require that c - R and c + R both be within the abscissa range [0,1] of the lobe, which is true. For verification, we have

Inellipse (lobe)

Using z = 1 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt [6sin(2t) - 5sin(4t) + sin(8t)]/8

has a zero at

The corresponding coordinates are

We then have

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle (lobe) R = 1.159273 0.106945 (0.632303,0)

Inellipse (lobe) a = 0.416666
b = 0.175345 1.937955 0.229526 (0.583334,0)

Rose 6.682447 0.785398

Convex hull 5.319609 1.610171

Circumcircle R = 1 6.283185 3.141593

Figure	Parameters	Perimeter	Area	Centroid
Incircle (lobe)	R =	1.159273	0.106945	(0.632303,0)
Inellipse (lobe)	a = 0.416666 b = 0.175345	1.937955	0.229526	(0.583334,0)
Rose		6.682447	0.785398
Convex hull		5.319609	1.610171
Circumcircle	R = 1	6.283185	3.141593

Top Page

Home