Nephroid

Nephroid NEPHROID

Balmoral Software

The nephroid is a two-cusped epicycloid S with parametric equations

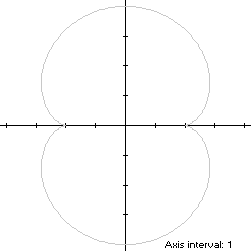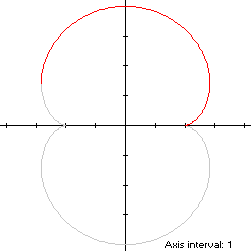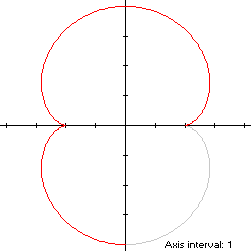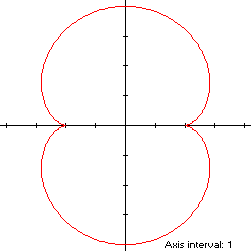
x(t) = 3cos(t) - cos(3t)
y(t) = 3sin(t) - sin(3t), 0 ≤ t < 2π

This bisymmetric curve is traced out in a counterclockwise direction around the origin, starting from the cusp at (2,0). Its maximum width occurs at the point pairs

which determine that the nephroid is non-convex by the multiple local extrema test. The values of t at these point pairs are ±π/4 (right pair) and ±3π/4 (left pair). The maximum height of the nephroid is between the point pair (0,±4), so the width x height of its bounding rectangle is

Metrics

The perimeter of the nephroid is 24 and its area A = 12π.

Convex Hull

The convex hull is created by connecting the extreme abscissa points with vertical line segments of length

as shown in blue in the left diagram below. We have

x'(t) = -3sin(t) + 3sin(3t)
y'(t) = 3cos(t) - 3cos(3t)

so by (L1), the perimeter of the convex hull is

which is about 6% shorter than that of the nephroid.

To compute the area of the convex hull, we can see by (A1) that the area A₁ of the region in green in the left diagram below is the integral of y dx from x = 2 at the cusp to at the maximum abscissa point:

Therefore, the area of the convex hull is

A + 4A₁ = 12π + 4(5 - 3π/2) = 20 + 6π = 38.849556,

which is about 3% more than the area of the nephroid.

Boundary Circles & Inellipse

The squared-distance function of S

x²(t) + y²(t) = 10 - 6cos(2t)

has its extrema on the coordinate axes at (±2,0) and (0,±4), so the inradius is 2 and the circumradius is 4. A candidate for the inellipse is one enclosed by the annulus between these two circles, with a = 2 and b = 4. For verification, we have

Circumellipse

From Lemma B,

x(t)y(t) = [9sin(2t) - 6sin(4t) + sin(6t)]/2

is maximized in the first quadrant when

The circumellipse dimensions are

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 2 12.566371 12.566371

Inellipse a = 2
b = 4 19.376896 25.132741

Nephroid 24 37.699112

Convex hull 22.627417 38.849556

Circumellipse 23.181126 41.848410

Circumcircle R = 4 25.132741 50.265482

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 2	12.566371	12.566371
Inellipse	a = 2 b = 4	19.376896	25.132741
Nephroid		24	37.699112
Convex hull		22.627417	38.849556
Circumellipse		23.181126	41.848410
Circumcircle	R = 4	25.132741	50.265482

Top Page

Home