Mouth Curve

Mouth Curve MOUTH CURVE

Balmoral Software

The "Mouth curve" is a bisymmetric sextic curve S with parametric equations

x(t) = cos(t)
y(t) = sin³(t), 0 ≤ t < 2π

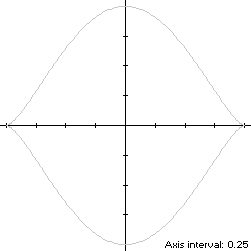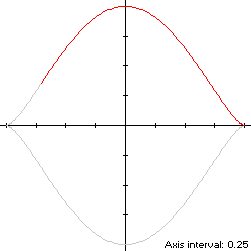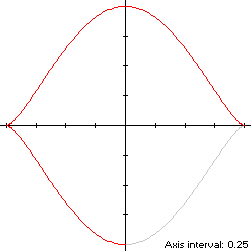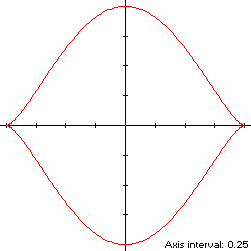
The curve is traced out in a counterclockwise direction, starting from its right-hand cusp at (1,0). Its abscissa extrema are (±1,0) and its ordinate extrema (0,±1), so its bounding rectangle is a 2 x 2 square.

Metrics

We have

x'(t) = -sin(t)
y'(t) = 3sin²(t)cos(t),

so by (L1), the perimeter of S is

By (A1), the area enclosed by S is

Convex Hull

We have

x''(t) = -cos(t)
y''(t) = 6sin(t) - 9sin³(t),

so by (X1), the curvature of S changes sign when t = 0 since that value is a solution to

-sin(t)[6sin(t) - 9sin³(t)] = -cos(t)[3sin²(t)cos(t)]

Equation (X2) is evaluated with respect to the point (x(0),y(0)) = (1,0) as

which has a solution in the first quadrant at t = π/3. The convex hull is created by connecting the points

and (1,0) with a straight line segment of length

and symmetrically in the other three quadrants. By (L1), the perimeter of the convex hull is:

which is about 0.4% shorter than the perimeter of S.

In the left figure below, the area of the Quadrant I portion of the triangle outlined in blue is

and the area of the remaining convex hull area in Quadrant I is

so the total area of the convex hull is

which is about 2% larger than the area of S.

Boundary Circles & Circumellipse

The squared distance function x²(t) + y²(t) ranges from

to 1, so the inradius is

and the circumradius is 1. Since the maximum distance of S from the origin along its positive and negative axes is the same, its circumellipse is the same as its circumcircle.

Inellipse

From Lemma B,

x(t)y(t) = cos(t)sin³(t)

is maximized in the first quadrant when t^* = π/3, so the inellipse dimensions are

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 4.927795 1.932393

Inellipse 5.128805 2.040524

Mouth curve Width: 2
Height: 2 5.82896 2.356195

Convex hull 5.805229 2.409196

Circumcircle R = 1 6.283185 3.141593

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R =	4.927795	1.932393
Inellipse		5.128805	2.040524
Mouth curve	Width: 2 Height: 2	5.82896	2.356195
Convex hull		5.805229	2.409196
Circumcircle	R = 1	6.283185	3.141593


The Aria

The mouth curve (red) is a member of a group of similarly-shaped figures described on these pages, including (inside to outside) the Vesica Piscis and the cycloid:

Top Page

Home