Balmoral Software
Balmoral Software

To find the radius R and center abscissa c of the larger circle, we have
which has solution
 So that S
is traversed in a clockwise direction starting from its left edge (-1,0) at
So that S
is traversed in a clockwise direction starting from its left edge (-1,0) at
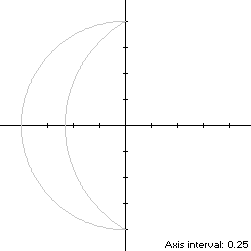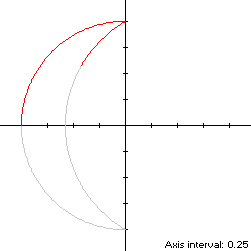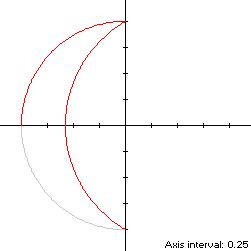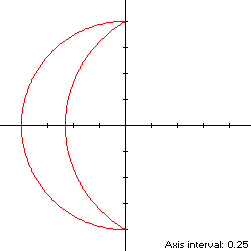
The abscissa maxima of the lune are at the two cusps (0,±1), so it is non-convex by the multiple local extrema test. The ordinate extrema are also at the cusps, so the width x height of the lune's bounding rectangle is 1 x 2. The lune crosses the x-axis at -1 and
so the perimeter of the convex hull is about about 8% shorter than that of the lune itself.
The portion of the unit semicircle that is not part of the lune is the segment of the larger circle, which has area
The centroid abscissa of this segment is
The lune metrics can be summarized as follows:
The convex hull has a little more than twice the area of the lune. The centroid abscissa of the lune is is the weighted average
Region Area Centroid abscissa Product Convex hull π/2 -4/(3π) -2/3 Segment Lune (by subtraction)
The bounding rectangle for inconics is delimited by the upper x-intercept
 occurring when
occurring when
 and the corresponding outer
ordinates
and the corresponding outer
ordinates 
 and center
abscissa
and center
abscissa  For verification, we
have
For verification, we
have
 in
Lemma E,
in
Lemma E,
has a zero at t* = π/6. The corresponding coordinates are:
so the inellipse dimensions are
For verification,
For verification,
Figure Parameters Perimeter Area Centroid Incircle R = 1.327793 0.140298 (-0.788675,0) Inellipse 2.572074 0.349066 (-0.769800,0) Lune Width: 1
Height: 25.559992 0.751883 (-0.628821,0) Convex hull 5.141593 1.570796 (-0.424413,0) Circumellipse 5.825171 2.418401 (-0.333333,0) Circumcircle R = 1 6.283185 3.141593
Copyright © 2021 Balmoral Software (http://www.balmoralsoftware.com). All rights reserved.