Isosceles Triangle

Isosceles Triangle ISOSCELES TRIANGLE

Balmoral Software

Consider a y-symmetric isosceles triangle with vertices (0,v) and (±u,0), u,v > 0. The width x height of its bounding rectangle is 2u x v.

Let t represent the usual parameter, ranging from 0 to 2π through the quadrants in counterclockwise order. The parametric equations of the triangle are piecewise linear in t:

Metrics

The lateral side length of the triangle is

so its perimeter is 2(u + s) and its area is uv. Its centroid is the average of its vertex coordinates: (0,v/3).

Incircle

The radius and center ordinate of the triangle's largest bounded circle (its incircle) are

R = d = u(s - u)/v

Inellipse

Using z = 0 in Lemma E,

d/dt x(t)[y(t) - z] = d/dt uv(1 - 2t/π)(1 - |1 - 2t/π|)

has a zero over [0,π) at t* = π/4. The corresponding coordinates are:

x* = u/2
y* = v/2,

so the inellipse dimensions are

For verification,

Circumellipse

Using h = v and w = 2u in Lemma TE, the parameters of the circumellipse are

Circumcircle

If the triangle is obtuse (u > v), its apex point (0,v) is not tangent to its bounding circle. In that case, the triangle's smallest bounding circle has a diameter between the vertices (±u,0) and its center at the origin.

If the triangle is acute (u ≤ v), then using h = v and w = 2u in Lemma TC, the circumellipse has radius and center ordinate

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = u(s - u)/v 2πR πR² (0,R)

Inellipse Computed (0,v/3)

Isosceles triangle Width: 2u
Height: v 2(u + s) uv (0,v/3)

Circumellipse Computed (0,v/3)

Bounding circle Obtuse: R = u 2πu πu²

Acute: R = 2πR πR² (0,v - R)

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = u(s - u)/v	2πR	πR²	(0,R)
Inellipse		Computed		(0,v/3)
Isosceles triangle	Width: 2u Height: v	2(u + s)	uv	(0,v/3)
Circumellipse		Computed		(0,v/3)
Bounding circle	Obtuse: R = u	2πu	πu²
Acute: R =	2πR	πR²	(0,v - R)

The centers of the boundary ellipses are both the same as the centroid of the isosceles triangle, and the circumellipse is exactly twice as large as the inellipse.

Specific Example

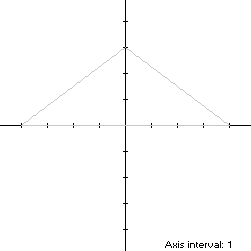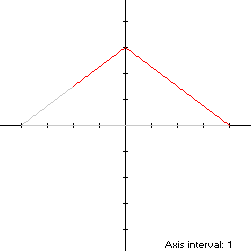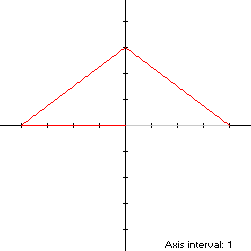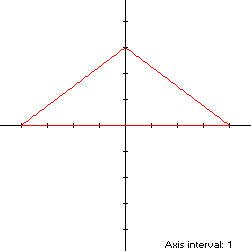
The boundary conics for an obtuse isosceles triangle with u = 4 and v = 3 are shown below:

Top Page

Home