Hippopede

Hippopede HIPPOPEDE

Balmoral Software

The hippopede, also known as the Lemniscate of Booth, is a peanut-shaped bisymmetric curve S with polar equation

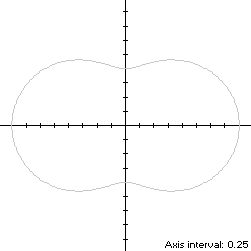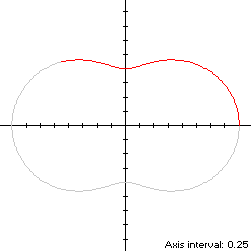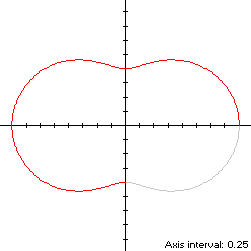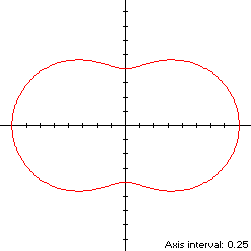
r²(t) = 4 - 3sin²(t), 0 ≤ t < 2π

The curve is traced out in a counterclockwise direction, starting from its right edge at (2,0). Its abscissa extrema are (±2,0) and its ordinate extrema

so the hippopede is non-convex by the multiple local extrema test. In the first quadrant, the ordinate maximum is achieved when

The width x height of its bounding rectangle is

Metrics

We have

so by (L2), the perimeter of S is

and by (A2), the area of S is

Convex Hull

The convex hull is created by connecting the extreme ordinate points with two horizontal line segments of length

so by (L2), the perimeter of the convex hull is

which is less than 1% shorter than that of the hippopede.

The line segments of the convex hull create two isosceles triangles with the origin, each having an area of

as shown in blue in the left diagram below. By (A2), the area of the convex hull is

which is about 3% more than the area of the hippopede.

Boundary Circles & Inellipse

The radius extrema are on the coordinate axes at (0,±1) and (±2,0), so the inradius is 1 and the circumradius is 2. A candidate for the inellipse is one enclosed by the annulus between these two circles, with a = 2 and b = 1. For verification, we have

Circumellipse

From Lemma B, we have

x(t)y(t) = [4 - 3sin²(t)]cos(t)sin(t)

This expression is maximized in the first quadrant at the complicated value

which is close to

The circumellipse dimensions are

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 1 6.283185 3.141593

Inellipse a = 2
b = 1 9.688448 6.283185

Hippopede 10.6941 7.853982

Convex hull 10.622106 8.076415

Circumellipse 10.955915 8.926023

Circumcircle R = 2 12.566371 12.566371

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 1	6.283185	3.141593
Inellipse	a = 2 b = 1	9.688448	6.283185
Hippopede		10.6941	7.853982
Convex hull		10.622106	8.076415
Circumellipse		10.955915	8.926023
Circumcircle	R = 2	12.566371	12.566371

Top Page

Home