Fish Curve

Fish Curve FISH CURVE

Balmoral Software

The fish curve is an x-symmetric ichthyic closed curve S with parametric equations

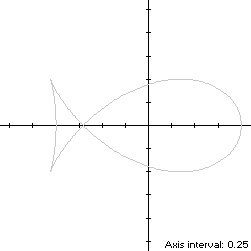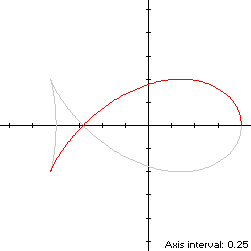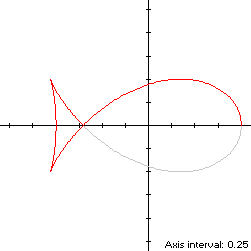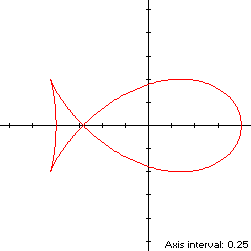
for t ∈ T = [0,2π). As t increases from 0, S starts from its right-hand edge at (1,0) and moves through Quadrants I and II, crossing the x-axis at

when t = π/2 and entering Quadrant III before reversing direction at the fin tip and returning to Quadrant II. It then reverses direction again and continues counterclockwise through Quadrants II, III and IV back to its starting point. The ordinate maxima of S occur at the top of the main lobe

when t = π/4 and at the fin tip

when t = 5π/4. Its minimum abscissas also occur at each fin tip, so S is non-convex by the multiple local extrema test. The width x height of its bounding rectangle is

Metrics

The perimeter of the fish curve is

and its area is 4/3. Its centroid is

Convex Hull

The convex hull is created by connecting the extreme ordinate and minimum abscissa points with two horizontal line segments of length

and one vertical line segment of length 1. We have

so by (L1) and symmetry, the perimeter of the convex hull is

which is about 13% shorter than that of the fish curve.

The line segments of the convex hull create a rectangle of area as shown in blue in the left diagram below. The centroid abscissa of this rectangle is the average of its vertex abscissas, or By (A1) and symmetry, the remainder of the convex hull has area

By (C1), the associated centroid abscissa is found by integrating

Since S is defined parametrically and is traced out in a counterclockwise direction, the usual limits of integration are reversed.

The convex hull component metrics can be summarized as follows:

Region Area Centroid abscissa Product

Rectangle -1/2

Remainder

Total

Region	Area	Centroid abscissa	Product
Rectangle			-1/2
Remainder
Total

The area of the convex hull is 1.927596, about 45% larger than that of the fish curve. The centroid abscissa of the convex hull is the weighted average

Circumcircle

Using z = 1 in Lemma C, we have

and

For verification, we have

Circumellipse

Lemma E does not produce an ellipse that fully contains S, so we resort to a numerical search to determine the optimal circumellipse:

a = 1.290478
b = 0.640445
c = -0.254244
d = 0

Incircle (main lobe)

The maximum radius of a circle centered on the x-axis and inscribed in S is its maximum ordinate, so a candidate for the main lobe incircle has radius R = 1/2 and center abscissa

The candidate circle must be contained within S, so we require that c - R and c + R both be within the abscissa range

of the main lobe of S, which is true. For verification, we have

Inellipse (main lobe)

Using z = 1 in Lemma E,

has a zero when t* is a complicated expression approximated by 1.083243 radians. The corresponding coordinates are

x* = -0.083459
y* = 0.413881,

from which we have

For verification,

Tail

Inconics can also be found for the tail portion of the fish curve, occurring when t ∈ T = [π/2,3π/2). The left edge of the tail at (-1,0) occurs at t = π when S revisits the x-axis for the third time.

Incircle (tail)

Using z = -1 in Lemma C, we have

Inellipse (tail)

Using z = -1 in Lemma E,

has a zero when t* is a complicated expression approximated by 1.749441 radians. The corresponding coordinates are

x* = -0.862475
y* = -0.174868,

from which we have

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle (tail) 0.774771 0.047768 (-0.876691,0)

Inellipse (tail) a = 0.091683
b = 0.201920 0.955186 0.058159 (-0.908317,0)

Incircle (main lobe) R = 1/2 3.141593 0.785398 (0.353553,0)

Inellipse (main lobe) a = 0.722306
b = 0.477908 3.809772 1.084465 (0.277694,0)

Fish curve 6.464082 1.333333 (0.141421,0)

Convex hull 5.646255 1.927596 (-0.129731,0)

Circumellipse a = 1.290478
b = 0.640445 6.239295 2.596464 (-0.254244,0)

Circumcircle 6.854894 3.739311 (-0.090990,0)

Figure	Parameters	Perimeter	Area	Centroid
Incircle (tail)		0.774771	0.047768	(-0.876691,0)
Inellipse (tail)	a = 0.091683 b = 0.201920	0.955186	0.058159	(-0.908317,0)
Incircle (main lobe)	R = 1/2	3.141593	0.785398	(0.353553,0)
Inellipse (main lobe)	a = 0.722306 b = 0.477908	3.809772	1.084465	(0.277694,0)
Fish curve		6.464082	1.333333	(0.141421,0)
Convex hull		5.646255	1.927596	(-0.129731,0)
Circumellipse	a = 1.290478 b = 0.640445	6.239295	2.596464	(-0.254244,0)
Circumcircle		6.854894	3.739311	(-0.090990,0)

The fish curve (red) is similarly shaped to the trefoil:

Top Page

Home