Epicycloid

Epicycloid EPICYCLOID

Balmoral Software

A three-lobed epicycloid is a closed curve S with parametric equations

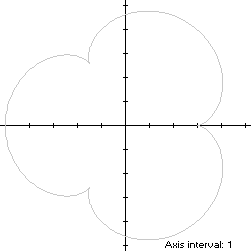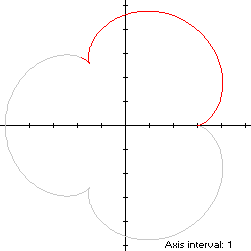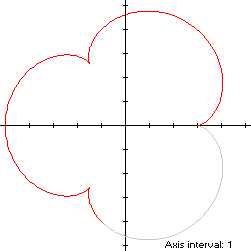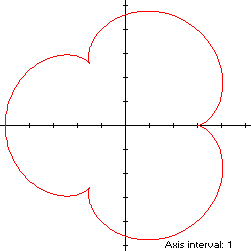
x(t) = 4cos(t) - cos(4t)
y(t) = 4sin(t) - sin(4t), 0 ≤ t < 2π

The curve is traced out in a counterclockwise direction, starting from its right cusp at (3,0). Its abscissa extrema are (-5,0) at t = π and

at t = ±π/5, so the epicycloid is non-convex by the multiple local extrema test. Its ordinate extrema are

at t = ±2π/5, so the width x height of its bounding rectangle is

Symmetry

Since

x(t + 2π/3) = cos(2π/3)x(t) - sin(2π/3)y(t)

and

y(t + 2π/3) = sin(2π/3)x(t) + cos(2π/3)y(t),

the conditions (R1) of Lemma R are satisfied and the epicycloid is rotationally symmetric with period 2π/3.

Metrics

We have

x'(t) = 4[sin(4t) - sin(t)]
y'(t) = 4[cos(t) - cos(4t)],

so by (L1), the perimeter of S is

and by (A1), the area of S is

Convex Hull

The convex hull is created by connecting the maximum abscissa points with a vertical line segment of length

and then repeating the pattern by rotating around the origin at 2π/3 intervals. By (L2), the perimeter of the convex hull is

which is about 8% shorter than that of the epicycloid.

To compute the area of the convex hull, we can see by (A1), that the area A₁ of the region in solid green in the left diagram below is the integral of y dx from x = 3 at the cusp to at the maximum abscissa point:

Therefore, the area of the convex hull is

which is about 4% more than the area of the epicycloid.

Boundary Circles & Circumellipse

Since the epicycloid is rotationally symmetric with period 2π/3, its circumcircle and circumellipse are the same. The squared-distance function of S

x²(t) + y²(t) = 17 - 8cos(3t)

ranges from 9 to 25, so its inradius is 3 and its circumradius is 5.

Inellipse

The lateral asymmetry of S permits an offset inellipse centered on the x-axis and tangent at all three cusps. The search program produces the optimal result

a = 2.453277
b = 4.712299
c = 0.546723
Perimeter = 23.074230
Area = 36.318614

Lobe Circumellipse

It's interesting that a lobe of the epicycloid is almost perfectly elliptical in shape, as indicated by the close-fitting brown ellipse in the left diagram below. The height of this x-symmetric ellipse is the maximum ordinate of S over the lobe parameter range 2π/3 ≤ t ≤ 4π/3:

The corresponding abscissa is the center of the ellipse:

For tangency at the left edge (-5,0), we have

To verify that this ellipse encloses the lobe of S, we have

The ellipse appears to pass through the points (0,±1), but this an illusion due to the limited resolution of the image, since

rather than 1. Although the ellipse is close-fitting, it is not the minimum-area circumellipse of the lobe, which can be found by numerical search:

a = 2.269858
b = 3.112156
c = -2.730142 = a - 5

and is shown in green in the left diagram below.

Summary Table

Figure Parameters Perimeter Area Centroid

Lobe ellipse a =
b = 17.335157 23.755802 (-2.427051,0)

Incircle R = 3 18.849556 28.274334

Inellipse a = 2.453277
b = 4.712299 23.074230 36.318614 (0.546723,0)

Epicycloid 32 62.831853

Convex hull 29.389263 65.552643

Circumcircle R = 5 31.415927 78.539816

Figure	Parameters	Perimeter	Area	Centroid
Lobe ellipse	a = b =	17.335157	23.755802	(-2.427051,0)
Incircle	R = 3	18.849556	28.274334
Inellipse	a = 2.453277 b = 4.712299	23.074230	36.318614	(0.546723,0)
Epicycloid		32	62.831853
Convex hull		29.389263	65.552643
Circumcircle	R = 5	31.415927	78.539816

Top Page

Home