Balmoral Software
Balmoral Software

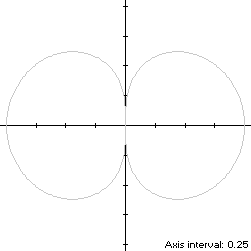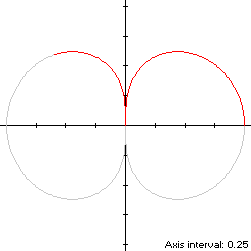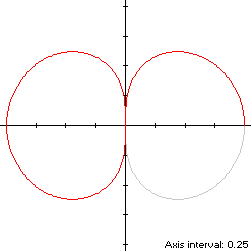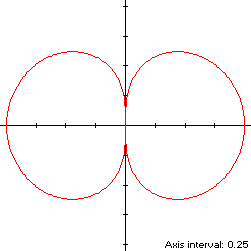
This bisymmetric curve is traced out in a counterclockwise direction around the origin, starting from the right edge at (1,0). Its maximum height occurs at the points
 which determine that the
dipole is non-convex by the multiple
local extrema test. The values of t at these points are
which determine that the
dipole is non-convex by the multiple
local extrema test. The values of t at these points are
 and π -
and π -
 . The maximum width of the
dipole is between the point pair (0,±1), so the width x height of its
bounding rectangle is
. The maximum width of the
dipole is between the point pair (0,±1), so the width x height of its
bounding rectangle is 
so by (L2), the perimeter of S is
and by (A2), the area of S is
 as shown in blue in the left
diagram below. By (L2), the perimeter of
the convex hull is
as shown in blue in the left
diagram below. By (L2), the perimeter of
the convex hull is
which is about 24% shorter than that of the dipole.
The line segments of the convex hull create two isosceles triangles with the origin, each having an area of
By (A2), the area of the convex hull is
which is about 9% more than the area of the dipole.
x(t)y(t) = r2(t)cos(t)sin(t) = |cos(t)|sin(2t)/2This expression is maximized in the first quadrant at
 The circumellipse dimensions are
The circumellipse dimensions are
For verification, we have
 so a candidate for a circle
inscribed in the lobe is one with a radius R and center abscissa c both equal to
1/2. For verification, we have
so a candidate for a circle
inscribed in the lobe is one with a radius R and center abscissa c both equal to
1/2. For verification, we have
d/dt [x(t) - z]y(t) = d/dt |cos(t)|sin(2t)/2We established in the preceding Circumellipse section that this expression has a zero in the first quadrant at
 The corresponding coordinates are
The corresponding coordinates are
We then have
For verification, we have
The value of c is negated in the diagram below to display the inellipse separately in the left lobe.
Figure Parameters Perimeter Area Centroid Incircle (lobe) R = 1/2 3.141593 0.785398 (0.5,0) Inellipse (lobe) 3.446495 0.930842 (0.491859,0) Dipole 7.16557 2 Convex hull 5.460413 2.177324 Circumellipse 5.636992 2.418399 Circumcircle R = 1 6.283185 3.141593
 |  |
| Thong? |
The dipole (red) is a member of a group of figure-8 curves described on these pages, including (inside to outside) the dumbbell curve, the bowtie, the Lemniscate of Bernoulli and the Lemniscate of Gerono:
Copyright © 2021 Balmoral Software (http://www.balmoralsoftware.com). All rights reserved.