Balmoral Software
Balmoral Software

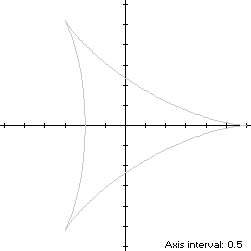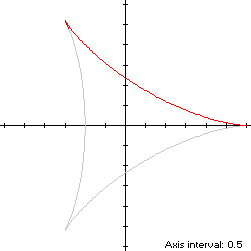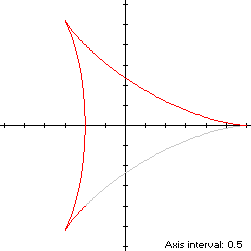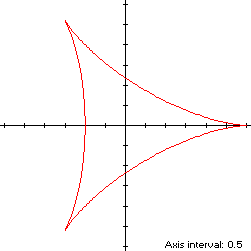
x(t) = 2cos(t) + cos(2t)The curve is traversed in a counterclockwise direction, starting at the right cusp (3,0) aty(t) = 2sin(t) - sin(2t), 0 ≤ t < 2π
 , it is non-convex by the
multiple local extrema test. The
width x height of its bounding rectangle is
, it is non-convex by the
multiple local extrema test. The
width x height of its bounding rectangle is
x(t + 2π/3) = cos(2π/3)x(t) - sin(2π/3)y(t)and
y(t + 2π/3) = sin(2π/3)x(t) + cos(2π/3)y(t),the conditions (R1) of Lemma R are satisfied and the deltoid is rotationally symmetric with period 2π/3.
x2(t) + y2(t) = 4cos(3t) + 5ranges from 1 to 9, so its inradius is 1 and its circumradius is 3.
d/dt [x(t) - z]y(t) = d/dt 4sin3(t)cos(t)has a zero at t = ±π/3. The corresponding points on S are
 Together with
Together with
 by line segments of length
by line segments of length
 , as shown in blue in the left
diagram below. The perimeter of the convex hull is
, as shown in blue in the left
diagram below. The perimeter of the convex hull is
 , which is about 3% shorter than
that of the deltoid. The area of the convex hull is half that of its bounding
rectangle:
, which is about 3% shorter than
that of the deltoid. The area of the convex hull is half that of its bounding
rectangle:
and is about 86% more than the area of the deltoid.
Figure Parameters Perimeter Area Centroid Incircle R = 1 6.283185 3.141593 Deltoid 16 6.283185 Convex hull 15.588457 11.691343 Circumcircle R = 3 18.849556 28.274334
Copyright © 2021 Balmoral Software (http://www.balmoralsoftware.com). All rights reserved.