Cycloid

Cycloid CYCLOID

Balmoral Software

Consider the closed convex shape S created from one cycloid arch, translated to the left by π and joined to its reflection across the x-axis. So that S is traversed in a counterclockwise direction around the origin starting from its right-hand corner (π,0) at t = 0, its parametric equations are

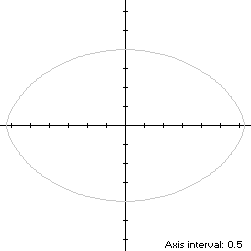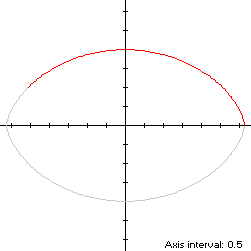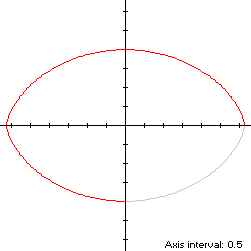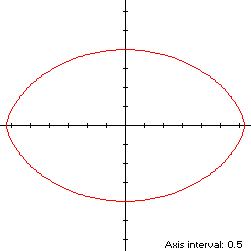
Since y(π - t) = y(t) and the path of the lower arch is a point reflection through the origin of the upper arch, S is bisymmetric. Its abscissa extrema are (±π,0) and its ordinate extrema (0,±2), so the width x height of its bounding rectangle is 2π x 4. Its perimeter is double that of one cycloid arch: 2(8) = 16, and similarly, its area is 2(3π) = 6π.

Boundary Circles & Circumellipse

The squared distance function x²(t) + y²(t) of S ranges from a minimum of 4 at (0,±2) to a maximum of π² at (±π,0), so the inradius is 2 and the circumradius is π. Since these extrema occur on the coordinate axes, a candidate for the circumellipse is one enclosed by the annulus between the two boundary circles, with a = π and b = 2. For verification, we have

Inellipse

In Lemma B, we have for the upper arch

x(t)y(t) = [-2t + π + sin(2t)][1 - cos(2t)]

This expression is maximized at

t* = 0.984995,

so the inellipse dimensions are

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 2 12.566371 12.566371

Inellipse a = 2.959917
b = 1.963884 15.627233 18.261870

Cycloid arches Width: 2π
Height: 4 16 18.849556

Circumellipse a = π
b = 2 16.352486 19.739211

Circumcircle R = π 19.739209 31.006277

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 2	12.566371	12.566371
Inellipse	a = 2.959917 b = 1.963884	15.627233	18.261870
Cycloid arches	Width: 2π Height: 4	16	18.849556
Circumellipse	a = π b = 2	16.352486	19.739211
Circumcircle	R = π	19.739209	31.006277

The cycloid (red) is a member of a group of similarly-shaped figures described on these pages, including (inside to outside) the mouth curve and the Vesica Piscis:

Top Page

Home