Cochleoid

Cochleoid COCHLEOID

Balmoral Software

A cochleoid having its cusp on the right is a heart-shaped x-symmetric closed curve S with even polar function

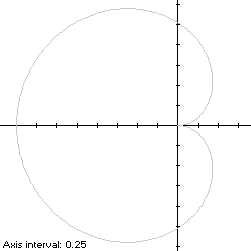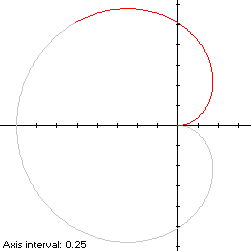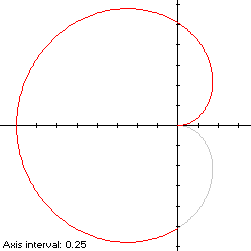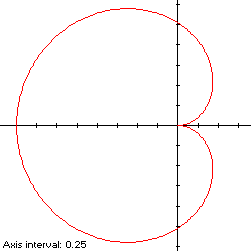
r(t) = -2sin(t)/t, t ∈ T,

where t is measured in radians. For a simple curve describing the outer envelope of the cochleoid, T is restricted to the interval [-π,π). The scaling factor -2 is used for comparison with the cardioid.

The curve is traced out in a counterclockwise direction, starting from the cusp at the origin when t = -π. Its minimum abscissa occurs at the limit point (-2,0) as t → 0. Its maximum abscissas occur at the points (0.434467,∓0.541786) when t = ±2.246705, which determine that the cochleoid is non-convex by the multiple local extrema test. The extreme ordinates of the cochleoid occur at the points (-0.621685,∓1.449223) when t = ±1.165561, so the width x height of its bounding rectangle is 2.434467 x 2.898446.

Metrics

We have

so by (L2), the perimeter of this portion of the cochleoid is

By (A2), the corresponding area is

By (C2), the centroid abscissa of this portion of the cochleoid is

The bounding rectangle for inconics is delimited by the cusp at the origin.

Convex Hull

The convex hull is created by connecting the maximum abscissa points with a vertical line segment of length 1.083572 at x = 0.434467. By (L2), the perimeter of the convex hull is

which is about 5% shorter than that of the cochleoid.

The line segment of the convex hull creates an isosceles triangle with the origin, having area

(0.434467)(0.541786) = 0.235388

as shown in blue in the left diagram below. The centroid abscissa of this triangle is the average of its vertex abscissas, or 2(0.434467)/3 = 0.289645. By (A2), the remainder of the convex hull has area

By (C2), the associated centroid abscissa is

The convex hull component metrics can be summarized as follows:

Region Area Centroid abscissa Product

Triangle 0.235388 0.289645 0.068179

Remainder A₁ = 5.53872 -4.21048/A₁ -4.21048

Total 5.774108 -4.142301

Region	Area	Centroid abscissa	Product
Triangle	0.235388	0.289645	0.068179
Remainder	A₁ = 5.53872	-4.21048/A₁	-4.21048
Total	5.774108		-4.142301

The area of the convex hull is about 2% larger than that of the cochleoid. The centroid abscissa of the convex hull is the weighted average -4.142301/5.774108 = -0.717392.

Incircle

A candidate incircle is located on the x-axis between the minimum abscissa -2 and the cusp at the origin, and so has radius R = 1 and center abscissa c = -1. For verification, we have

Inellipse

Using z = 0 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt 4sin³(t)cos(t)/t²

has a zero at t* = -0.671886. The corresponding coordinates are

x* = -1.45016
y* = 1.15335

We then have

For verification,

Circumellipse

Using z = -2 in Lemma E,

d/dt [x(t) - z]y(t) = d/dt [-2sin(t)cos(t)/t + 2]2sin²(t)/t

has a zero at t* = -π/2. The corresponding coordinates are

x* = 0
y* = 4/π

We then have

For verification,

Circumcircle

The radius of a circle centered on the x-axis and circumscribing S is at least its maximum ordinate, so a candidate for the circumcircle has radius R = 1.449223 and center abscissa c = -0.621685. For verification,

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 1 6.283185 3.141593 (-1,0)

Inellipse a = 0.966773
b = 1.331774 7.266693 4.044873 (-0.966773,0)

Cochleoid Width: 2.434467
Height: 2.898446 9.056693 5.672606 (-0.736250,0)

Convex hull 8.603362 5.774108 (-0.717392,0)

Circumellipse 8.812839 6.158400 (-0.666667,0)

Circumcircle R = 1.449223 9.105737 6.598122 (-0.621685,0)

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 1	6.283185	3.141593	(-1,0)
Inellipse	a = 0.966773 b = 1.331774	7.266693	4.044873	(-0.966773,0)
Cochleoid	Width: 2.434467 Height: 2.898446	9.056693	5.672606	(-0.736250,0)
Convex hull		8.603362	5.774108	(-0.717392,0)
Circumellipse		8.812839	6.158400	(-0.666667,0)
Circumcircle	R = 1.449223	9.105737	6.598122	(-0.621685,0)

The cochleoid (red) is a member of a group of similarly-shaped figures described on these pages, including (inside to outside) the rotated lima bean curve, the cardioid and the Cayley sextic:

Top Page

Home