Bowtie

Bowtie BOWTIE

Balmoral Software

The bowtie is a figure-8 curve with polar equation

p(t) = 2 sin(2t) + 1, 0 ≤ t < 2π

Rotating the curve clockwise by π/4 produces the equivalent bisymmetric curve S with polar equation

r(t) = p(t + π/4) = 2 cos(2t) + 1, 0 ≤ t < 2π

The corresponding implicit function can be found by replacing cos(t) with x/r and r with x² + y²:

(x² + y²)³ = (3x² - y²)²

The corresponding parametric functions are:

x(t) = 2cos(t) + cos(3t)
y(t) = sin(3t)

Movement along S is always counterclockwise, crossing the origin four times. At t = 0, the path starts at the maximum abscissa point (3,0) and moves through Quadrant I along its right lobe to its maximum ordinate point

at t = π/6, and then on to the origin at t = π/3. It continues along the lower small lobe, returning to the origin at t = 2π/3. Next, it travels along the left lobe through Quadrant II to another maximum ordinate point

at t = 5π/6, then on to its minimum abscissa point (-3,0) at t = π and back to the origin at t = 4π/3. The path continues through the upper small lobe, including a third maximum ordinate point (0,1) at t = 3π/2, the origin and Quadrant IV back to its starting point at t = 2π:

t: 0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6 2π

x(t): 3 0 0 0 - -3 - 0 0 0 3

y(t): 0 1 0 -1 0 1 0 -1 0 1 0 -1 0

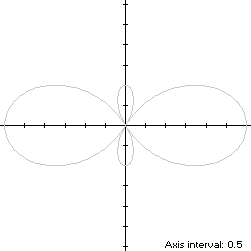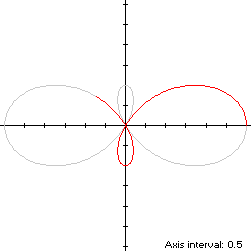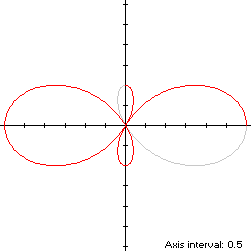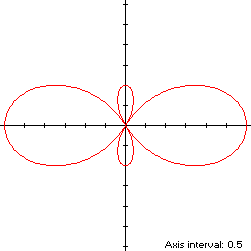
Since S has three maximum-ordinate points, it is non-convex by the multiple local extrema test. The width x height of the bowtie's bounding rectangle is 6 x 2.

Metrics

We have

r'(t) = -4 sin(2t),

so by (L2), the perimeter of S is

and by (A2), the area of S is

Convex Hull

The convex hull is created by connecting the extreme ordinate points with two horizontal line segments of length

each of which is bisected by another extreme ordinate point on one of the small lobes. By (L2), the perimeter of the convex hull is

which is about 30% shorter than that of the bowtie.

The line segments of the convex hull create two isosceles triangles with the origin, each having an area of

as shown in blue in the left diagram below. By (A2), the area of the convex hull is

which is about 16% more than the area of the bowtie.

Circumcircle

The radius maximum is 3, so that is the circumradius.

Circumellipse

From Lemma B, we have

x(t)y(t) = [2cos(t) + cos(3t)]sin(3t)

This expression is maximized in the first quadrant at the complicated value

The circumellipse dimensions are

For verification, we have

Incircle (lobe)

Consider the right lobe of the bowtie, where -π/3 ≤ t < π/3. The maximum radius of a circle centered on the x-axis and inscribed in the lobe is the maximum ordinate 1 of S, so a candidate for the lobe incircle has radius R = 1 and center abscissa

The circle must be contained within the lobe, so we require that c - R and c + R both be within the abscissa range [0,3] of the lobe, which is true. For verification, we have

Inellipse (lobe)

Using z = 3 in Lemma E,

d/dt [x(t) - z]y(t) = 2 cos(2t) - 9 cos(3t) + 4 cos(4t) + 3 cos(6t)

has a zero at t* = 0.711832. The corresponding coordinates are

x* = 0.979171
y* = 0.844749

We then have

For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle (lobe) R = 1 6.283185 3.141593 (1.732051,0)

Inellipse (lobe) a = 1.347219
b = 0.975432 7.343639 4.128431 (-1.652781,0)

Bowtie Width: 6
Height: 2 20.015781 9.424778

Convex hull 14.098791 10.935821

Circumellipse a = 3.262063
b = 1.268192 14.930224 12.996524

Circumcircle R = 3 18.849556 28.274334

Figure	Parameters	Perimeter	Area	Centroid
Incircle (lobe)	R = 1	6.283185	3.141593	(1.732051,0)
Inellipse (lobe)	a = 1.347219 b = 0.975432	7.343639	4.128431	(-1.652781,0)
Bowtie	Width: 6 Height: 2	20.015781	9.424778
Convex hull		14.098791	10.935821
Circumellipse	a = 3.262063 b = 1.268192	14.930224	12.996524
Circumcircle	R = 3	18.849556	28.274334

The bowtie curve (red) is a member of a group of figure-8 curves described on these pages, including (inside to outside) the dumbbell curve, the Lemniscate of Bernoulli, the Lemniscate of Gerono and the dipole:

Top Page

Home

t:	0	π/6	π/3	π/2	2π/3	5π/6	π	7π/6	4π/3	3π/2	5π/3	11π/6	2π
x(t):	3		0	0	0	-	-3	-	0	0	0		3
y(t):	0	1	0	-1	0	1	0	-1	0	1	0	-1	0