Bifolium

Bifolium BIFOLIUM

Balmoral Software

The bifolium is a two-lobed y-symmetric closed curve with polar equation

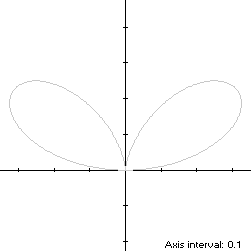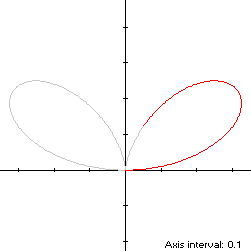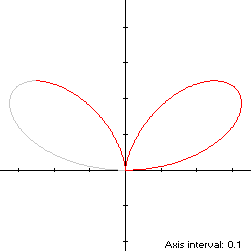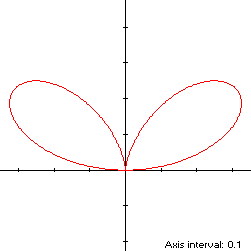
r(t) = sin(t)cos²(t), 0 ≤ t < π

The curve is traced out in a counterclockwise direction, starting from its minimum ordinate point at the origin when t = 0 and reaching its maximum abscissa point

at t = π/6. It reaches the first of its maximum ordinate points at t = π/4 before returning to the origin at t = π/2 and repeating the pattern symmetrically in the left half-plane. Since the bifolium has two maximum ordinate points at (±1/4,1/4), it is non-convex by the multiple local extrema test. The width x height of its bounding rectangle is

which has an aspect ratio of about 2.6.

The lobes of the bifolium (red) are spread farther apart than those in the upper half-plane of the comparably-sized four-leaved rose (black):

Metrics

The area of the bifolium is π/32 and its perimeter is 1.788887. Its centroid is the point (0,1/8).

Convex Hull

The convex hull is created by connecting the maximum ordinate points with a horizontal line segment of length 1/2 at y = 1/4. We have

r'(t) = 3cos³(t) - 2cos(t),

so by (L2), the perimeter of the convex hull is

which is about 14% shorter than that of the bifolium.

The line segment of the convex hull creates an isosceles triangle with the origin, having an area of (1/4)² = 1/16, as shown in blue in the left diagram below. The centroid ordinate of this triangle is the average of its vertex ordinates, or 1/6. By (A2), the remainder of the convex hull has area

By (C2), the associated centroid ordinate is

The convex hull component metrics can be summarized as follows:

Region Area Centroid ordinate Product

Triangle 1/16 1/6 1/96

Remainder A = (4 + 3π)/192

Total (16 + 3π)/192

Region	Area	Centroid ordinate	Product
Triangle	1/16	1/6	1/96
Remainder	A = (4 + 3π)/192
Total	(16 + 3π)/192

The area of the convex hull is 0.132421, about 1/3 larger than that of the bifolium. The centroid ordinate of the convex hull is the weighted average

Circumcircle

The parametric coordinate functions of the bifolium are

x(t) = r(t)cos(t) = sin(t)cos³(t)
y(t) = r(t)sin(t) = sin²(t)cos²(t) = sin²(2t)/4

The radius of a circle centered on the y-axis and circumscribing the bifolium is at least its maximum abscissa, so a candidate for the circumcircle has radius

and center ordinate d = 3/16. For verification,

Circumellipse

Using z = 0 in Lemma E,

d/dt x(t)[y(t) - z] = d/dt sin³(t)cos⁵(t)

has a zero at t* = Arccos(1/4)/2. The corresponding coordinates are

We then have

For verification,

Lobe

Unlike the lobe of a rose, the bifolium lobe is asymmetric with respect to its maximum-radius axis (which is also the case for the lobes in the tail of the trefoil). To see this, rotate the bifolium clockwise so that the spine of its right lobe is oriented along the x-axis. To determine the angle of rotation, we begin by finding the maximum radius point of the bifolium in Quadrant I, which occurs at

when

Since the bifolium is defined by a polar function, t_R is also the clockwise rotation angle. The parametric coordinate functions of the rotated curve are:

x(t) = r(t)cos(t - t_R)
y(t) = r(t)sin(t - t_R)

The asymmetry can then be seen by comparing the upper half of the lobe (red) with a reflection of the lower half (blue):

Incircle (lobe)

Since the lobe is asymmetric, we resort to an unconstrained numerical search over the lobe parameter range 0 ≤ t < π/2 to determine the optimal lobe incircle:

R = 0.087970
c = 0.189708
d = 0.139099

Inellipse (lobe)

An inellipse can be found by first using an unconstrained numerical search of the rotated lobe defined by the equations above over the parameter range 0 ≤ t < π/2 to determine an optimal axis-aligned inellipse with an off-axis center:

a = 0.165788
b = 0.084029
c = 0.217709
d = 0.005909

To display the tilted ellipse in the left lobe for comparison with the incircle, we negate c and then rotate the ellipse clockwise by t_R = 35.26439° to produce the result in the left-hand diagram below. This approach presupposes that the major axis of the ellipse is along the spine of the lobe, which produces a slightly suboptimal inellipse.

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle (lobe) R = 0.087970 0.552732 0.024312 (0.189708,0.139099)

Inellipse (lobe) * a = 0.165788
b = 0.084029 0.805983 0.043766 (0.217709,0.005909)

Bifolium 1.788887 0.098175 (0,0.125)

Convex hull 1.530382 0.132421 (0,0.199639)

Circumellipse 1.646991 0.171504 (0,0.15625)

Circumcircle R = 2.040524 0.331340 (0,0.1875)

*: With respect to rotated curve S

Figure	Parameters	Perimeter	Area	Centroid
Incircle (lobe)	R = 0.087970	0.552732	0.024312	(0.189708,0.139099)
Inellipse (lobe) *	a = 0.165788 b = 0.084029	0.805983	0.043766	(0.217709,0.005909)
Bifolium		1.788887	0.098175	(0,0.125)
Convex hull		1.530382	0.132421	(0,0.199639)
Circumellipse		1.646991	0.171504	(0,0.15625)
Circumcircle	R =	2.040524	0.331340	(0,0.1875)


Visitor from the planet Bifolium

Top Page

Home