Bicorn

Bicorn BICORN

Balmoral Software

The bicorn is a y-symmetric closed curve S with a shape reminiscent of the bicorne hat worn by Napoleon and others. It is defined by the parametric equations

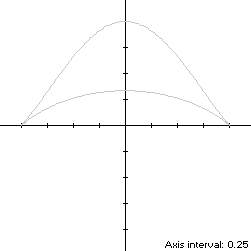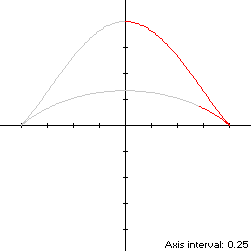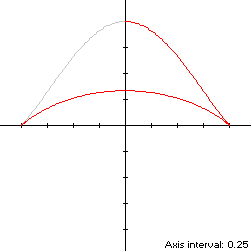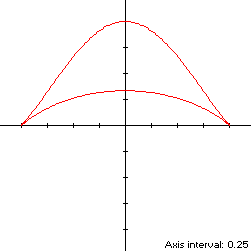
The curve follows a clockwise path as t increases, starting from its maximum ordinate at (x(0),y(0)) = (0,1), reaching its maximum abscissa (1,0) at t = π/2, then the local height maximum (0,1/3) at t = π and the minimum abscissa (-1,0) at t = 3π/2 before returning to the y-axis. Since two ordinate minima occur on the x-axis, the bicorn is non-convex by the multiple local extrema test, and the width x height of its bounding rectangle is 2 x 1.

Metrics

The perimeter of the bicorn is approximately 5.056530 and its area is

Its centroid ordinate is

The bounding rectangle for inconics is delimited by the lower y-intercept y(t) = 1/3 occurring when t = ±Arccos(2/3) and the corresponding outer abscissas

Convex Hull

The convex hull is created simply by connecting the two cusps of the bicorn with a horizontal line segment of length 2. We have

x'(t) = cos(t)
y'(t) = sin(t){1 - 4/[cos(t) - 2]²},

so by (L1), the perimeter of the convex hull is

which is about 3% shorter than that of the bicorn.

By (A1), the area A of the convex hull is determined by integrating over the same subinterval of T:

which is about 62% larger than the area of the bicorn.

By (C1), the centroid ordinate of the convex hull is

Incircle

A candidate incircle is located between the ordinate extrema of S on the y-axis, and so has radius R = 1/3 and center ordinate d = 2/3. For verification, we have

Inellipse

Using z = 1/3 in Lemma E,

d/dt x(t)[y(t) - z] = d/dt sin(t){cos²(t)/[2 - cos(t)] - 1/3}

has a zero at

The corresponding coordinates are

We then have

For verification,

Circumellipse

Using z = 1 in Lemma E,

d/dt x(t)[y(t) - z] = d/dt sin(t){cos²(t)/[2 - cos(t)] - 1}

has a zero at t* = π/2. The corresponding coordinates are

x* = 1
y* = 0,

from which we have

For verification,

Circumcircle

Since the abscissa extrema are on the x-axis and the bounding rectangle is wider than it is tall, a candidate for the circumcircle has radius 1 and center at the origin. For verification, we have

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 1/3 2.094395 0.349066 (0,0.666667)

Inellipse a = 0.470553
b = 0.289332 2.421315 0.427715 (0,0.622665)

Bicorn Width: 2
Height: 1 5.056530 0.746456 (0,0.542011)

Convex hull 4.90528 1.210026 (0,0.386245)

Circumellipse 5.825171 2.418399 (0,0.333333)

Circumcircle R = 1 6.283185 3.141593

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 1/3	2.094395	0.349066	(0,0.666667)
Inellipse	a = 0.470553 b = 0.289332	2.421315	0.427715	(0,0.622665)
Bicorn	Width: 2 Height: 1	5.056530	0.746456	(0,0.542011)
Convex hull		4.90528	1.210026	(0,0.386245)
Circumellipse		5.825171	2.418399	(0,0.333333)
Circumcircle	R = 1	6.283185	3.141593


	Koala Frog

Top Page

Home