Arbelos

Arbelos ARBELOS

Balmoral Software

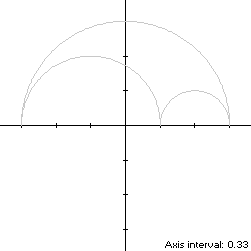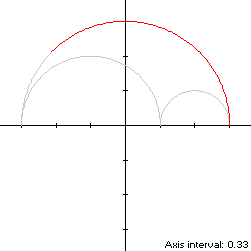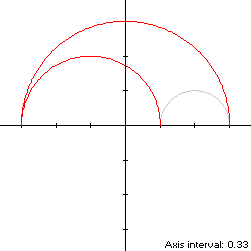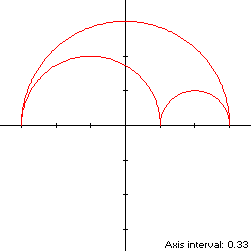
Consider the arbelos S with left radius r and right radius 1 - r, 0 < r < 1, and therefore with enclosing radius 1, oriented so that the center of the enclosing semicircle is at the origin. Then the centers of the left and right semicircles are (r - 1,0) and (r,0) respectively. S is asymmetric if r ≠ 1/2.

So that S is traversed in a counterclockwise direction starting from its right edge (1,0) at t = 0, its parametric equations can be written:

Metrics

The perimeter of the arbelos is the sum of the semicircumferences of circles of radius 1, r and 1 - r, or 2π, the perimeter of a unit circle (the answer from WolframAlpha is in error by a factor of 2). Its area is that of a unit semicircle, less the areas of the two smaller semicircles, or r(1 - r)π, which ranges from 0 to π/4.

Using the formula for the centroid of a semicircle, the arbelos metrics can be summarized as follows:

Region Area Centroid Product

Unit semicircle π/2 (0,4/(3π)) (0,2/3)

Left semicircle r²π/2 (r - 1,4r/(3π)) (r²(r - 1)π/2,2r³/3)

Right semicircle (1 - r)²π/2 (r,4(1 - r)/(3π)) (r(r - 1)²π/2,2(1 - r)³/3)

Arbelos (by subtraction) r(1 - r)π (r(1 - r)(2r - 1)π/2,2r(1 - r))

Region	Area	Centroid	Product
Unit semicircle	π/2	(0,4/(3π))	(0,2/3)
Left semicircle	r²π/2	(r - 1,4r/(3π))	(r²(r - 1)π/2,2r³/3)
Right semicircle	(1 - r)²π/2	(r,4(1 - r)/(3π))	(r(r - 1)²π/2,2(1 - r)³/3)
Arbelos (by subtraction)	r(1 - r)π		(r(1 - r)(2r - 1)π/2,2r(1 - r))

The centroid of the arbelos is the weighted average

(r(1 - r)(2r - 1)π/2,2r(1 - r))/[r(1 - r)π] = (r - 1/2,2/π)

Since the arbelos has three cusps, it is non-convex by the multiple local extrema test. The width x height of its bounding rectangle is that of the unit semicircle, 2 x 1.

Convex Hull

The convex hull of the arbelos is created simply by connecting its three cusps with a horizontal line segment of length 2, as shown in blue in the left diagram below. The perimeter of the convex hull is half the circumference of a unit circle plus the line segment, or π + 2, which is about 18% shorter than the perimeter of the arbelos. The area of the convex hull is that of a unit semicircle, or π/2, which is always at least twice the area of the arbelos itself. The centroid of the convex hull is that of a unit semicircle centered at the origin, as shown above: (0,4/(3π)). When r is greater than 8/(9π²) + 1/2 = 0.59, the centroid of the convex hull is outside of the arbelos.

Circumellipse

The extreme points of the arbelos create a y-symmetric isosceles triangle with vertices at (0,1) and (±1,0). Using h = 1 and w = 2 in Lemma TE, a candidate for the circumellipse has parameters

The parametric equations of the convex hull of S are:

For verification,

Circumcircle

Since the arbelos is a portion of a unit circle centered at the origin, its circumcircle is that circle.

Incircle

Denote the radius and center of the largest circle inscribed in the arbelos as R and (c,d), as shown in the diagram above. Since the points of tangency of the incircle with the left and right semicircles lie along lines connecting their centers, we have

[c - (r - 1)]² + (d - 0)² = (r + R)²
(c - r)² + (d - 0)² = (1 - r + R)²

By "Surprise No. 7" in [10], a vertical line from (c,d) to the horizontal base of the arbelos is bisected by the lower arc of the incircle; or equivalently,

d = 2R

Solving the preceding three equations simultaneously for R, c and d yields

Specific Example

In the remainder of this paper, we use r = 2/3 as illustrated in the diagram above. Then the metrics of the incircle are:

R = 2/7
(c,d) = (3/7,4/7)

and the centroid of the arbelos is (1/6,2/π).

Inellipse

Since it's evident that an optimal inscribed ellipse will be tilted downwards toward the smallest semicircle, we can formulate an equivalent problem by rotating the arbelos itself by a counterclockwise angle -φ to orient its inellipse in a rectilinear position. This ellipse will be tangent to each of the smaller semicircles and twice tangent to the enclosing semicircle, and is y-symmetric. A numerical search can be used to determine the optimal tilted inellipse:

φ = -25.514°
a = 0.592932
b = 0.236724
c = 0.318006
d = 0.666294
Area = 0.440957

Summary Table

Figure Parameters Perimeter Area Centroid

Incircle R = 2/7 1.795196 0.256457 (0.428571,0.571429)

Inellipse a = 0.592932
b = 0.236724 2.728001 0.440957 (0.318006,0.666294)

Arbelos Width: 2
Height: 1 6.283185 0.698132 (0.166667,0.636620)

Convex hull 5.141593 1.570796 (0,0.424413)

Circumellipse 5.825171 2.418401 (0,0.333333)

Circumcircle R = 1 6.283185 3.141593

Figure	Parameters	Perimeter	Area	Centroid
Incircle	R = 2/7	1.795196	0.256457	(0.428571,0.571429)
Inellipse	a = 0.592932 b = 0.236724	2.728001	0.440957	(0.318006,0.666294)
Arbelos	Width: 2 Height: 1	6.283185	0.698132	(0.166667,0.636620)
Convex hull		5.141593	1.570796	(0,0.424413)
Circumellipse		5.825171	2.418401	(0,0.333333)
Circumcircle	R = 1	6.283185	3.141593

Top Page

Home